이항계수

이항 계수는 주어진 크기의 주어진 크기 집합에서 원하는 개수만큼 순서없이 뽑는 조합의 가짓수이다.

  • 전체 집합에서 원소의 개수 n에 대해 k개의 아이템을 뽑는 이항계수(조합의 수)는 다음과 같이 정의한다.

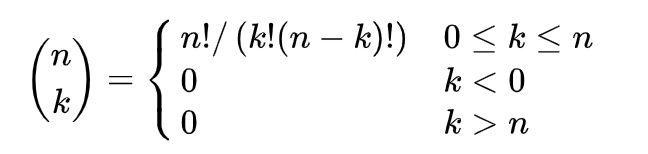
Alt binomial

  • 이항 계수의 값을 삼각형 모양으로 나열한 표를 파스칼의 삼각형이라고 한다.

Alt binomial

이항계수의 성질

  • 이항 계수는 다음과 같은 항등식을 만족한다.

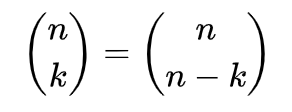
Alt binomial

  • 그리고 다음과 같은 점화식이 성립하며, 이는 파스칼의 법칙이라 한다.

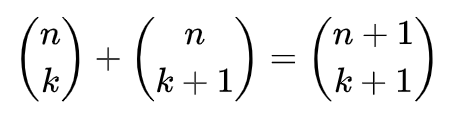
Alt binomial

이항계수의 구현

  • 이항계수의 구현은 Recusion의 관점에서 접근할 수 있다.
    • Base Case : if n == k or k ==0 일 때는 0
    • Recursion Case : (n-1 K) + (n-1 k-1)
      • 점화식에서 (n k) = (n-1 K) + (n-1 k-1)을 도출해낼 수 있다.
    • Recusion 방식이므로 많은 중복 계산이 수행된다.
function binomial(n, l) {
  if (n == k || k == 0) {
    return 1;
  } else {
    return binomial(n - 1, k) + binomial(n - 1, k - 1);
  }
}

Memoization을 통한 개선

function binomial(n, l) {
  if (n == k || k == 0) {
    return 1;
  } else if (binom[n][k] > -1) {
    //binom은 -1로 초기화 되었다고 가정
    return binom[n][k];
  } else {
    binom[n][k] = binomial(n - 1, k) + binomial(n - 1, k - 1);
    return binom[n][k];
  }
}

참고